2. Analyse de Styx : section D
La grande densité d'attaques de cette section pose un problème intéressant à notre perception qui peut se résumer dans une question : est-ce que les processus écrits dans la partition sont évidents à l'écoute ? En d'autres mots, est-ce qu'il nous est possible de séparer les différentes couches qui composent la trame sonore ? Pour traiter ces questions, nous ferons des calculs qui nous permettront de connaître le résultat approximatif des superpositions présents dans cette section.

Figure 7. Mâche, Styx (D), superposition des quatre derniers tempi.
Pour avoir une idée de la densité, il est intéressant de connaître la quantité d'attaques dans le processus le plus dense de la section, le dernier. Pour arriver à ce résultat, on va étudier le morceau comprenant la superposition des quatre derniers tempi ; c'est-à-dire, à partir de l'entrée du pianiste 2 avec le tempo noire = 184. Tout ce morceau dure 33 secondes environ. Voyez la Figure 7.
Les quatre tempi superposés sont les suivants : noire = 168 (pianiste 1), noire = 184 (pianiste 2), noire = 138 (pianiste 3), noire = 152 (pianiste 4). Comme chaque pianiste joue toujours des croches, il faut prendre en considération le double d'attaques pour chaque pianiste : 336 (pianiste 1), 368 (pianiste 2), 276 (pianiste 3) et 304 (pianiste 4).
Pour connaître la quantité d'attaques, il est nécessaire d'additionner les attaques des quatre pianistes mais aussi de soustraire ceux qui sont coïncidents [1].

Figure 8. Mâche, Styx (D), dernier processus, superposition des tempi de pianistes 1 (noire = 168, croche = 336) et 2 (noire = 184, croche = 368).
Lorsqu'on superpose les tempi des pianistes 1 (noire = 168) et 2 (noire = 184), on observe qu'il y a 16 attaques qui sont coïncidents. Plus spécifiquement, la superposition 21 croches sur 23 croches se répète 16 fois avec une durée approximative de 3, 75 secondes (60 secondes divisé par 16). Voyons la Figure 8.
Ainsi, il faut faire le calcul suivant : 336 + 368 - 16 = 688. Cela veut dire que, si on superpose ces deux tempi, on aura 688 attaques dans une minute.
Maintenant, il faut savoir si, quand on ajoute les tempi du pianiste 3 (noire = 138, croche = 276) et du pianiste 4 (noire = 152, croche = 304) il y a des coïncidences avec les autres deux tempi que nous venons de voir.
Concrètement, lorsqu'on fait un calcul similaire à celui qu'on vient de faire on constate que le tempo du pianiste 3 ajoute 176 attaques dans une minute (100 attaques sont coïncidentes). Donc, 688 + 276 - 100 = 864. Le pianiste 4 a 16 attaques coïncidentes avec les autres, donc : 864 + 304 - 16 = 1152. Si le nombre d'attaques dans une minute est de 1152, dans une seconde il y a 1152 divisé par 60 = 19,2.
Lorsqu'on observe la Figure 9, on voit que les quatre tempi suivent un modèle qui se répète quatre fois, de façon identique, dans une minute.
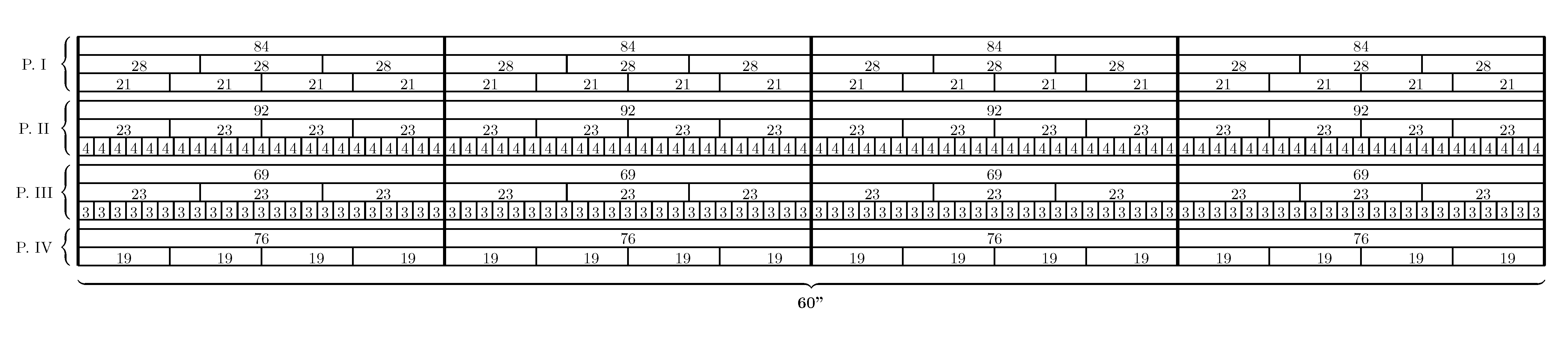
Figure 9. Mâche, Styx (D), dernier processus, superposition des tempi des quatre pianistes (1, noire = 168, croche = 336 ; 2, noire = 184, croche = 368 ; 3, noire = 138, croche = 276 ; 4, noire = 152, croche = 304).