La Tonalité : un cercle du diable
Les théories du système tonal sont, depuis le début du XIXe siècle, fondées sur ce qui pourrait être considéré, en partie, comme un malentendu : la tonalité existe parce qu'on y trouve l'enchainement de tels degrés de l'échelle. Cependant, l'on conviendra qu'il est impossible de déterminer a priori quels sont ces degrés, si la tonalité n'est pas elle-même définie.
La notion de progression harmonique
L'originalité de la théorie de Schönberg [1], déjà initiée par celles d'Öttingen [2]et de Tiersch [3], consiste probablement dans l'intérêt qu'elle porte à la distance entre les catégories tonales triadiques. Ces théories formulent un objet, une triade conceptuelle, d'une certaine manière 'abstractisée' pour pouvoir rendre compte, de manière précise, par la conduite des voix (les concepts de maintien en place des sons communs, du plus court chemin ou d'harmonies médiatrices). Les relations y sont décrites comme des combinaisons de tierce et de changement de mode, parce qu'elles sont les plus économiques. En comparaison, les lois de la progression sont envisagées avec Weber, Sechter et comme se réduisant aux modèles cadentiels (Stufenlehren), selon les fonctions qu'elles occupent dans un syntagme.
Arnold Schönberg est probablement un des premiers théoriciens de la tonalité qui considère la relation entre les entités harmoniques comme prévalant sur la nature des entités elles-mêmes. En effet, ainsi que l'écrit Nicolas Meeùs, à propos de la « conception typiquement atomiste » caractéristique du passé, « ce qui détermine la fonction d'un accord, ce n'est pas tant le degré sur lequel il se construit que la façon dont il est amené et quitté ; ce qui détermine la tonalité, c'est moins la fonction que l'on peut attribuer à chacun des accords que la signification tonale qui découle de leur succession » [4]. Dès son traité d'harmonie écrit en 1911, Schönberg insiste longuement sur la nécessité de prendre davantage en compte ces aspects que, depuis, de nombreux théoriciens considèrent comme fondamentaux pour la compréhension du système tonal, et également pour celle de la post-tonalité chromatique. D'une certaine manière, la théorie d'Arnold Schönberg ne semble pas, dans un premier temps, distinguer la tierce majeure de la tierce mineure. De ce point de vue, Harmonielehre effectue un retour vers le concept de fonction riemannienne. En effet, l'enchaînement de tierces identiques ne pouvant aboutir à une chute de quinte juste ou pas de quarte ascendante, la nature d'une relation de tierce ne dépendra pas uniquement du profil ascendant ou descendant de l'intervalle. Pour identifier de quelle progression précise il s'agit, il est nécessaire de connaître, outre la nature de la tierce séparant les basses fondamentales des harmonies mises en relation, la nature de la tierce harmonique des accords de départ et d'arrivée. Dans l'ouvrage Structural Functions of Harmony [5], il modifie la classification et apporte un éclairage nouveau, en définissant davantage le terme de « progression », notamment dans une opposition à celui de « succession ». La progression devient une forme particulière de succession harmonique, ayant un objectif défini, qu'elle peut servir ou contredire.
Le franchissement de la frontière
Le franchissement de la frontière entre harmonie et tonalité repose sur une définition imprécise des niveaux de la structure tonale et une croyance en un transfert direct de l'une à l'autre. Cette extension du processus au-delà des contours des simples événements successifs induit une zone d'ambiguïté entre accord et tonalité. Ainsi, Arthur von Öttingen [6] observe, répertorie et classifie les progressions harmoniques comme des combinaisons de tierce et de changement de mode qui, par définition, ne peuvent être considérées comme relevant de la même tonalité. Otto Tiersch [7] entretient cette même confusion entre catégories tonales d'échelles différentes, mais développe une théorie originale de la parenté selon une gradation de sons communs ou en rapports réciproques, plus ou moins signifiants, à partir de laquelle est évalué le dynamisme de la relation.
La notion de monotonalité
Cependant, que ce soit à propos de sa distinction entre progression et succession, ou de sa description insuffisamment précise des relations de tierce, Schönberg reste lui aussi tributaire de l'esprit des Stufenlehren qui lui ont été transmises par Bruckner. La théorie de la monotonalité et des régions tonales est elle-même également sous-tendue par le concept de fonction et de distance entre le degré secondaire promu au rang de tonique locale, et la tonique principale : chaque modulation entretient avec la tonalité principale les mêmes rapports que les harmonies secondaires correspondantes avec l'accord de tonique. Schönberg nomme chaque accord altéré, empruntant à une zone tonale autre, une transformation [8]. Ces transformations provenant de l'usage de substitutions des notes mélodiques à l'intérieur des échelles diatoniques, produisent des sensibles artificielles, qui, tout en ne modifiant pas les fonctions de la tonalité principale, doivent être rattachées à leur zone tonale d'origine. Outre la contradiction apparaissant entre ces deux perceptions opposées du phénomène « modulant », la théorie monotonale développée par Schönberg entraîne des conséquences non négligeables : même si elle constitue un progrès du point de vue de l'appréhension totale d'une partition, elle pourrait induire que ce qui se produit à l'échelle locale des harmonies se reproduit à celle plus générale des tonalités. En étendant la théorie des degrés au niveau des régions tonales, Schönberg pénètre un peu plus profondément encore la frontière mise à mal par Tiersch et Öttingen. Ce faisant, il n'explique pas davantage la nature intrinsèque du système, mais en diffère l'évaluation et présuppose une prétendue récursivité des niveaux composant sa structure.
La notion de transformation
Ce sont probablement les théories dites néo-riemanniennes qui, les premières, articulent leur pensée autour du concept de transformation d'unités harmoniques simples, les triades majeures et mineures ou les accords de septième, via une conduite parcimonieuse des voix favorisant les notes communes et obéissant à la loi du plus court chemin. Elles définissent ces transformations au sein d'un système chromatique fondé sur l'équivalence enharmonique. À l'époque de la tonalité stricte, ces paradigmes servaient essentiellement à l'étude d'une structure encore conçue comme diatonique, régie par une tonalité unifiée par les principes de la fonction dynamique et de la progression de la basse fondamentale. Cependant, et cela dès le second tiers du XIXe siècle, se faisaient déjà sentir de nouvelles approches de l'analyse du système tonal, probablement consécutives à l'évolution progressive de la pratique de la tonalité, notamment depuis les dernières compositions de Ludwig van Beethoven et de Franz Schubert. Ainsi, dès le milieu du siècle, Adolf Bernhard Marx [9] déplace le débat sur les progressions harmoniques, de l'étude des relations entre basses fondamentales à celle de la conduite mélodique des différentes voix entre chaque accord. Cette tendance ne fera que s'amplifier tout au long du XIXe siècle, et la trame théorique dans laquelle Hugo Riemann [10] décrit les relations entre deux tonalités voisines doit autant au concept de fluidité mélodique via les substitutions intervalliques, qu'à celui de la fonction tonale. C'est pourtant dans un tout autre cadre que certains théoriciens néo-riemanniens reprennent les descriptions du XIXe siècle, en les débarrassant des concepts de tonalité unifiée et de basse fondamentale qui les sous-tendaient, et en les dotant de structures nouvelles aptes à la description exhaustive des propriétés des objets observés. Ils introduisent dans leurs théories une logique chromatique, là où elle n'existait probablement pas encore. En effet, Riemann considérait le système comme diatonique, et les changements de mode comme résultant de sa structure dualiste.
Le système Schritt / Wechsel
L'ouvrage de David Lewin Generalized Musical Intervals and Transformations [11] constitue probablement l'un des actes fondateurs de la nouvelle école nommée néo-riemannienne. En reliant les trois transformations REL (Relative), LT (Leittonwechsel), PAR (Parallel), effectuées sur les triades consonantes à la grille de lecture dualiste de la théorie de Hugo Riemann, Lewin crée le cadre conceptuel nécessaire à leur interprétation en termes d'inversion contextuelle. C'est également dans l'héritage de Riemann et d'Öttingen, que Klumpenhouwer [12], revisite le système Schritt / Wechsel indépendant de l'environnement tonal, le distinguant de la théorie des fonctions harmoniques. Les théoriciens néo-riemanniens soutiennent que, dans la mesure où les constituants ne sont pas liés à une organisation diatonique du système, leurs transformations restent également indépendantes, réduisant la définition du réseau génératif à un ensemble de modifications apportées à un accord A permettant d'obtenir un accord B. Brian Hyer [13] reprend à son compte les catégories conceptuelles de la théorie de Arthur von Öttingen, et ramène l'ensemble des transformations de la triade à trois inversions contextuelles, le passage à l'accord des tons relatif (transformation REL ou R), contre-relatif résultant du change de sensible (transformation LT ou L) et parallèle (transformation PAR ou P), et à une transposition (transformation DOM), celle à la sous-dominante / dominante. Enfin, et ceci ne constitue pas le moindre de ses avantages, la pensée néo-riemannienne se dote d'outils formalisés, empruntés aux théories ensemblistes des mathématiques, permettant l'étude plus systématique des propriétés des structures harmoniques au sein du système relationnel dans lequel opèrent ces transformations. Le maintien des notes communes peut désormais s'exprimer en termes d'intersection et de cardinalité, et la fluidité mélodique se mesurer en nombre de demi-tons à l'intérieur d'un ensemble chromatique fermé par l'équivalence enharmonique de ses composants. Dès lors, les collections diatoniques et chromatiques, comme les triades ou les accords de septième, deviennent le produit de transformations autonomes sélectionnées et répertoriées pour leurs vertus symétriques, formalisables via un modèle.
La conduite des voix et le Tonnetz généralisé
C'est en 1996 que Richard Cohn [14] relie les trois inversions contextuelles R, L, P à une conduite parcimonieuse des voix, ce qui lui permet de définir un modèle théorique et une représentation générique de ces transformations qu'il appelle « PLR family » [15]. Il démontre, en remontant à une formulation générique du modèle PLR, que les collections triadiques consonantes mineures et majeures sont celles qui permettent la meilleure parcimonie. Ầ partir de la définition la plus générale d'un tricorde, comme ensemble des trois classes de hauteurs 0, x et x+y, il montre que, quelle que soit la collection harmonique, la transformation P génère une inversion des première et troisième classes, respectivement 0 et (x+y), et déplace la deuxième à une distance de (y-x), alors que L génère une inversion des première et deuxième classes (respectivement 0 et x) en provoquant le déplacement de la troisième à distance de (-2y-x), et que R génère une inversion des deuxième et troisième classes (respectivement x et (x+y)), en provoquant le déplacement de la première à distance de (2x+y). Cependant, au-delà de l'étude des relations harmoniques entre triades parfaites, c'est bien celle des relations entre toutes formes d'accords à trois ou quatre sons, que visent les néo-riemanniens, grâce aux concepts de transformation et de parcimonie. Parce qu'elles considèrent que la potentialité relationnelle entre entités harmoniques est due aux propriétés combinatoires de celles-ci à l'intérieur d'un espace chromatique, et non à d'autres propriétés préexistantes, grammaticales (tonalité) ou acoustiques (consonance), leurs théories sont en mesure d'évaluer des répertoires post-triadiques et post-tonals.
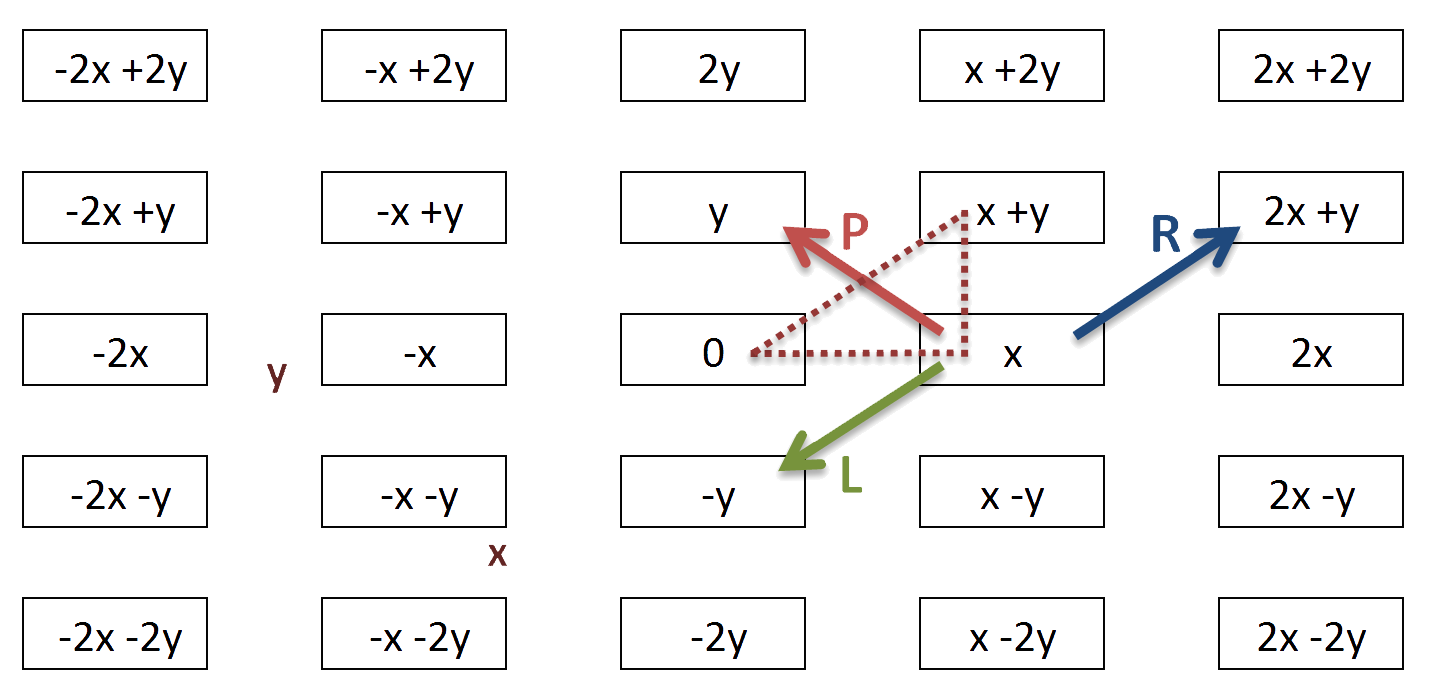
Figure 1 : Tonnetz généralisé
Grâce à la définition générique de certains concepts, comme celui de la cardinalité (c), et de la série d'intervalles entre les composants des tricordes (<x,y,-(x+y)>), Cohn parvient à établir le répertoire des chaînes de relations qu'il nomme « générateurs », ainsi qu'à systématiser le calcul de leur longueur et de leur fréquence, sur la base de notions aussi formalisées qu'une opération composée, que son classement parmi les transformations basiques de la Set Theory (transposition ou inversion), qu'un générateur, qu'un cycle et qu'une propriété d'involution ou de dévolution. Cohn conclut que les potentialités des triades sont davantage dues aux propriétés théoriques de leur groupe dans le cadre du tempérament égal et du chromatisme modulo 12, et ajoute même que ces propriétés combinatoires ont été, au cours de l'histoire, précisément masquées par la focalisation sur les propriétés acoustiques. Il soutient que, l'idée même selon laquelle une œuvre se fonde nécessairement sur un système unique, était à l'origine d'une conception unitaire de la tonalité, laquelle à son tour, avait pu constituer un obstacle à l'adaptation des concepts riemanniens au monde musical du dernier tiers du XIXe siècle et de la première moitié du XXe siècle. Grâce notamment aux nouvelles applications des concepts de Riemann, le tabou de la binarité « tonalité/atonalité » s'effondrait bientôt. Il ne devenait, dès lors, plus impensable de pénétrer un peu plus la frontière, considérée trop souvent comme imperméable, entre tonalité et modalité, et de déplacer ainsi la réflexion sur l'existence de systèmes à références et à fonctionnements multiples. Dans le cadre des mises en réseau selon la fluidité mélodique, et consécutivement aux études systématiques menées sur la relation entre progression harmonique et parcimonie, de nombreuses représentations voient le jour.
Par exemple, le Cube Dance constitue une reformulation des régions de Weitzmann [16], et connecte par conduite chromatique stricte les quatre triades augmentées deux à deux. Ces triades qui sont des collections à transpositions limitées, dont la résolution est multiple et étendue, compte tenu de leur formulation enharmonique, constituent aussi les fondamentales d'un cycle hexatonique PL.
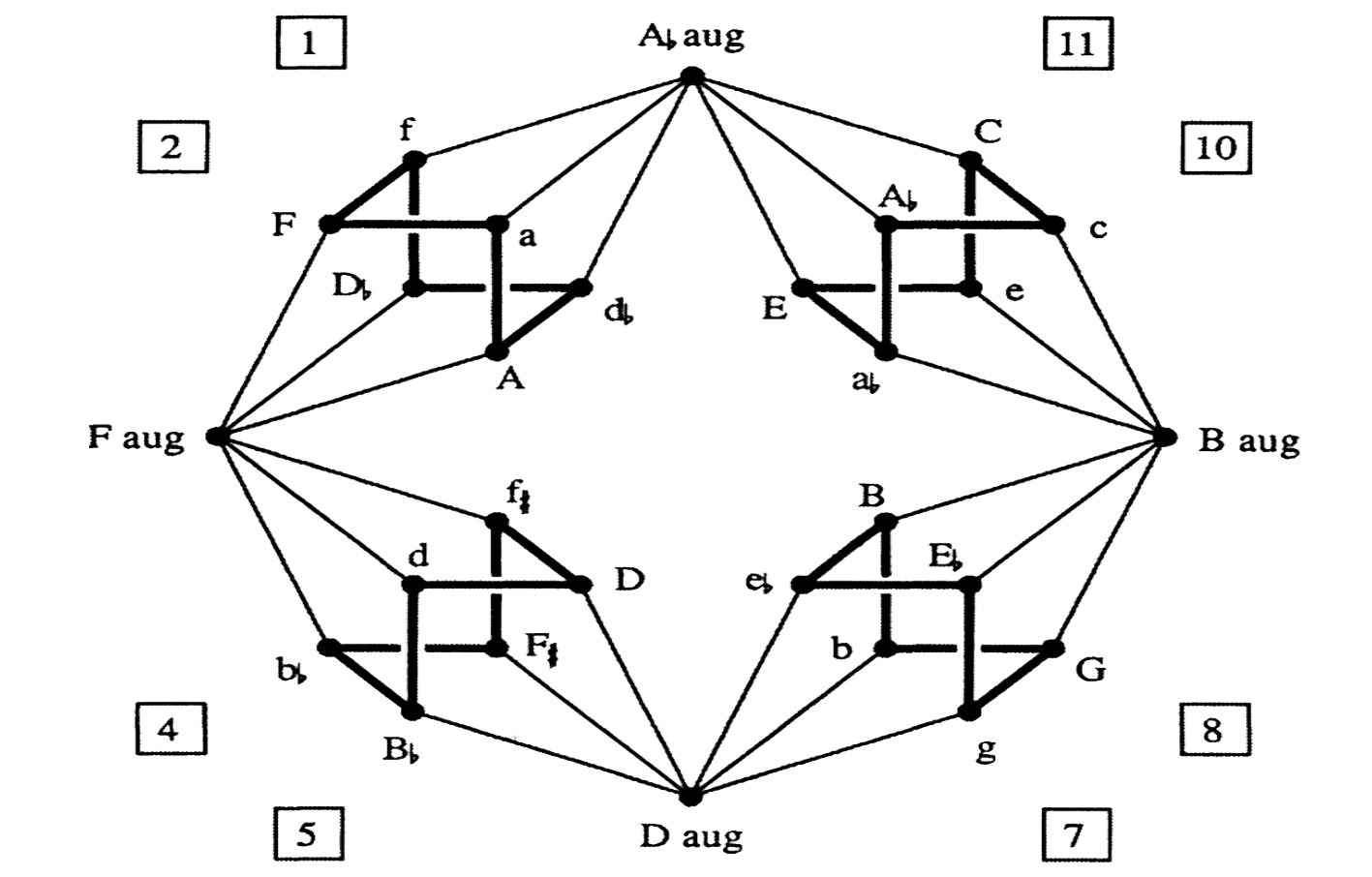
Figure 2 : Cube Dance
Dans cet autre graphe appelé « Chicken-wire torus » de Douthett et Steinbach [17], les transformations P sont orientées NO/SE (ligne continue), les transformations L (ligne pointillée serrée) NE/SO, alors que les transformations R sont horizontales (ligne pointillée large). Les « Hexacycles » (PL) sont représentées comme des lignes zigzagantes NO/SE et NE/SO. Les « Octacyles »(PR) allient lignes horizontales et obliques NO/SE. Ce graphe peut être considéré comme le point de départ d'autres représentations qui permettent de visualiser le passage d'une collection à une autre selon des cycles (Enneacycles, Octatowers), des Tonnetz de triades majeures et mineures, et d'accords de septième (Adrian Childs) [18].

Figure 3 : Chicken Wire
La représentation des régions tonales
La carte des régions d'Arnold Schönberg est très différente des autres représentations antérieures. La première de ses spécificités consiste en la distinction de la nature, majeure ou mineure, des harmonies ou régions mises en relation. De ce point de vue, la carte des régions de Schönberg manifeste certaines ressemblances avec des représentations passées (cf. Weitzmann) [19]. Les cartes majeure et mineure s'articulent toutes deux autour d'un axe vertical de quintes justes et d'un axe horizontal de tierces mineures. Pour chaque région, il existe deux colonnes, l'une majeure, l'autre mineure, de telle façon que sur l'axe des tierces mineures, les rapports harmoniques alternent tons parallèles et tons relatifs. La deuxième divergence de fond est l'absence d'un lien direct entre tonalités situées à distance de tierce majeure. Alors qu'Öttingen et Riemann conçoivent leurs cartes comme des représentations de hauteurs mises en relation selon des cycles intervalliques, Schönberg cherche à visualiser les liens entre des triades ou des harmonies, c'est à dire des ensembles de hauteurs. L'espace chromatique n'y est pas constitué d'aires géométriques délimitées par des segments intervalliques communs à deux figures adjacentes. Certes, l'observation du système tonal, jusque dans les premières années du XXe siècle, montre une structure harmonique majoritairement fondée sur des mouvements de quinte descendante de la fondamentale des accords. Néanmoins, les excursions effectuées hors de la diatonie par le moyen des notes communes entre les harmonies, dirigent souvent le plan tonal vers des régions éloignées, qu'une simple description par quintes aurait tendance à rapprocher artificiellement, ou dont un simple modèle transformationnel ne permettrait pas d'appréhender la polarité. Soumettre un corpus non strictement tonal à une évaluation des distances et des directions tonales pose les questions de la définition et des limites du système.
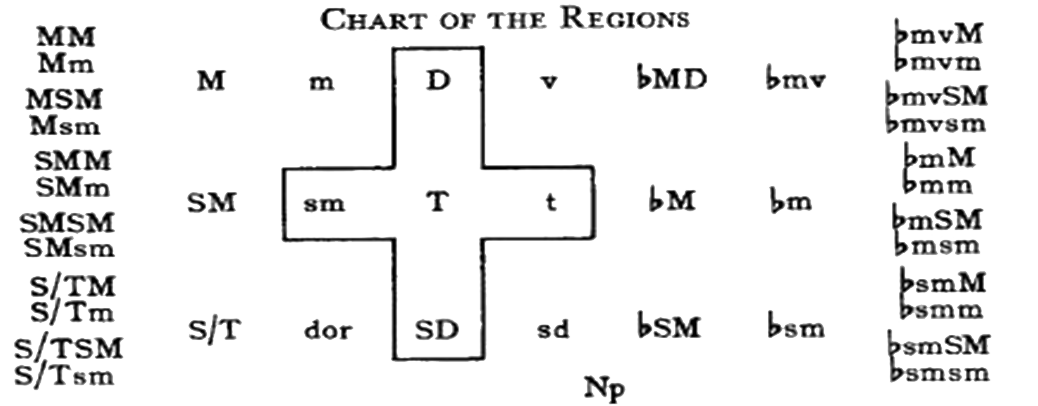
Figure 4 : carte des régions tonales